The quality of the tasks students are given, coupled with the quality of instruction they receive, has been shown to be one of the most powerful predictors of student achievement. Together these two constructs are called opportunity to learn, which has also been shown to be the single most important factor in explaining differences in achievement among different groups of students (Hiebert & Grouws, 2007). Relatedly, level of cognitive demand has proven to be a useful way to describe both the tasks teachers select and how they are implemented. Walter Doyle (1988) classified tasks as the context for students thinking both before and after instruction. In addition, he defined cognitive demand as the cognitive processes required of a student to be successful with a task.
In mathematics education there exists a strong correlation between giving students frequent opportunities to solve challenging mathematical problems, justify their reasoning, and chances to make connections between mathematical ideas, and increased student outcomes. It has also been shown that in order for students to engage in these practices, they need regular opportunities to work on cognitively demanding tasks (Stein & Lane, 1996). This includes evidence that cognitively demanding tasks increase learning opportunities for all students, not just those who were previously high-achieving (Zohar & Dori, 2003). Tasks with high cognitive demand tend to be open-ended, require students to make connections to underlying mathematical ideas, and engage students in the disciplinary practices mentioned above. In contrast, tasks with low cognitive demand require students to memorize or reproduce facts, or to perform relatively routine procedures without making connections to any underlying mathematical concepts.
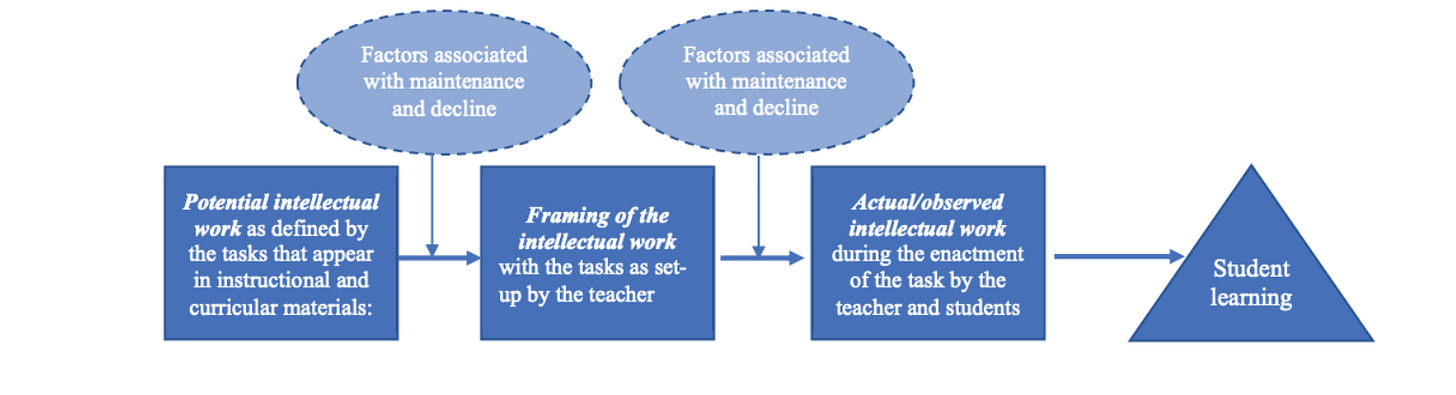
Stein et al., (2000) expanded the notion of task by proposing that the cognitive demand inherent to a task is not static, but rather a dynamic construct that is affected by the interactions teachers and students have with each other, as well as with the content in a classroom environment. The Task Framework (pictured below), depicts tasks as existing in different phases.
Source: Tekkumru‐Kisa, M., Stein, M.K., & Doyle, W. (2020).
The first phase, shown in the far left rectangle, represents the potential intellectual work, or cognitive demand of a task, as it exists in the curriculum, unit plan, or some other source. The next phase, shown immediately to the right of the initial rectangle, represents the task as set up or launched by the teacher. In other words, how a teacher takes the task as it exists on paper and brings it to life in the classroom. The oval between these two phases represents the factors associated with either reducing or maintaining the cognitive demand of the task as it moves from curriculum to classroom. The third rectangle in the figure (moving from left to right), represents the actual intellectual work that students are engaged in while working on the task. Again, the oval between the setup phase and this final phase represents the factors associated with either reducing or maintaining the cognitive demand of the task through transition. The far right triangle in the framework represents the actual student learning that occurs as a result of engaging in the task, with the goal being that the closer the final cognitive demand level of the task is to the intended demand level, the more learning will have taken place.
Despite its importance, maintaining the cognitive demand of a task through all phases of instruction has proven to be extremely challenging (Boston & Smith, 2009; Jackson, 2013; Munter & Haynes, 2019). Multiple studies have documented both the relatively few opportunities American students have to engage in cognitively demanding tasks, as well as the frequent reduction of demand that often occurs during implementation. For example, an analysis of a random sample of classroom video that was part of the 1999 TIMMS study found that American teachers selected tasks with a high level of potential cognitive demand only 17% of the time, and that of the tasks selected, the level of cognitive demand was maintained during implementation less than 1% of the time. Similarly, Jackson’s (2013) analysis of a large sample of middle school mathematics lessons revealed that the cognitive demand of many tasks was reduced in the launch phase (64% of the time), and only 6.7% of tasks that were launched effectively also maintained their potential level of cognitive demand through all phases of the lesson. Other research has shown that marginalized students receive fewer opportunities to engage in high cognitive demand tasks than their more privileged peers (Rubie-Davies, et al., 2014), and that students of color are more likely than their white classmates to perceive the reduction of the cognitive demand of a task over the course of a lesson to be related to teacher expectations based on their race (Munter & Haynes, 2019).
Classroom Connection
There are many factors related to maintaining or reducing the cognitive demand of a task during instruction. This post will not get into them all, but I will focus on a few that have proved to be both pernicious and prevalent. The factor most associated with reducing the demand of a task is the teacher removing some element of challenge for students in order to make the task easier and often much more procedural (Henningsen & Stein 1997). Catalysts for this reduction in challenge have been traced to things like teachers acquiescing to student pleas to make the task less ambiguous, which often removes opportunities for student sensemaking to occur. Other factors driving this lowering of demand also include teacher expectations, and teachers prioritizing task completion over productive struggle (Stein,Grover, & Henningsen, 1996).
Conversely, one of the factors most associated with the maintenance of cognitive demand is teacher press for explanation and justification (Menzies, Schunn, & Stein, 2024). This often involves teachers asking questions to probe student thinking, as well as prompting students to provide reasons or justifications for their answers or proposed next steps. These types of interactions have been shown to successfully surface student misconceptions, engage students in metacognitive processes, and support students in connecting mathematical actions and procedures to overarching concepts and ideas (Warshauer, 2015). Additionally, Wilhelm (2014) found that a teacher's ability to maintain the cognitive demand of a task throughout all phases of instructions is highly correlated to their understanding of effective instruction, level of mathematical knowledge for teaching, and views on the capabilities of struggling students.
While there is no doubt that tasks with high potential cognitive demand are necessary for sustained student success, they are in no way sufficient. As this post has illustrated, a student's opportunity to learn also hinges on whether the cognitive demand of a task is maintained throughout instruction. Unfortunately, maintenance of cognitive demand continues to be difficult to achieve. Without careful attention to how tasks are launched, facilitated, and consolidated, the cognitive demand can easily be diminished, limiting the depth of student learning. Supporting teacher efficacy in this area is crucial, as it serves as a powerful leverage point in creating more equitable outcomes and greater overall student success in mathematics.
Related Reads
This article examined teacher responses to student struggle and provides a framework for how teachers can respond to student struggle without reducing cognitive demand.
This article provides a rich summary of the research base on the implementation of cognitively demanding tasks in mathematics.
This study demonstrates the importance of an effective task launch, showing that it serves as a leading indicator for the level of cognitive demand students experience for the remainder of the lesson.
This article examined how students of color perceived the decline of cognitive demand over the life of a task as compared to their white classmates.
This chapter, by Hiebert and Grouws, discusses the construct of opportunity to learn and its relationship to student outcomes.
This is a link to The Task Analysis Guide, which is a useful tool for classifying the potential cognitive demand of a math task.
This link takes you to a resource I wrote to assist teachers in launching cognitively demanding tasks. It is part of a series of instructional recipes I authored, which you can find on my website via this link.