The Core of the Matter Issue #11
Scaffolding student learning without diluting challenge: Connecting cognitive load and cognitive demand…
This issue explores an important challenge for teachers: how to provide support for students during instruction without lowering the cognitive demand of the task? This brings together two concepts that I’ve discussed before—cognitive load and cognitive demand. This is a crucial and difficult challenge as research consistently highlights how hard it is for teachers to strike this balance effectively and consistently (Sullivan & Mornane, 2014). In fact, Stein et al. (1996) found that in their sample of math classrooms, scaffolds that reduced cognitive demand were provided 64% of the time during task enactment. But first, a quick review of these concepts.
Cognitive demand refers to the kind of thinking a task requires for students to be successful (Doyle, 1988). It captures how much students must figure out; how hard they must think to complete the task. When a task is aligned to important learning goals, this demand reflects germane cognitive load, or the mental effort relevant to the intended learning. For more on cognitive demand, see Issue #9.
Cognitive load, on the other hand, is concerned with how to best manage the limited capacity of working memory during the learning process. Unlike our long-term memory, our working memory has an extremely limited capacity and can become overloaded quickly. During knowledge acquisition, our working memories deploy resources to think about all kinds of things, also known as cognitive load, some of which are connected to what we are trying to learn and some that are not. For more on cognitive load, see Issue #4. Therefore, another way of looking at maintaining cognitive demand is to think about it in terms of maximizing the germane load of a task while minimizing extraneous load that distracts or overwhelms.
Further, in relation to cognitive load, scaffolding refers to any instructional move that reduces extraneous cognitive load. That is, unnecessary mental effort that distracts from the core learning goal. Cognitive Load Theory is a helpful lens for evaluating whether a proposed support is a true scaffold: one that reduces extraneous load without interfering with germane load, or the mental effort directly tied to the learning objective. If a support reduces germane load, it likely lowers the cognitive demand of the task and would not be considered effective in promoting meaningful learning.
As discussed in Issue 4, scaffolds typically take two main forms: tools and strategic prompts, both of which can help reduce extraneous load. Tools might include resources like books on tape, graphic organizers, or math manipulatives. Strategic prompts, on the other hand, guide novice learners’ attention toward the most germane aspects of a task, helping them stay focused on the core reasoning at the heart of the work.
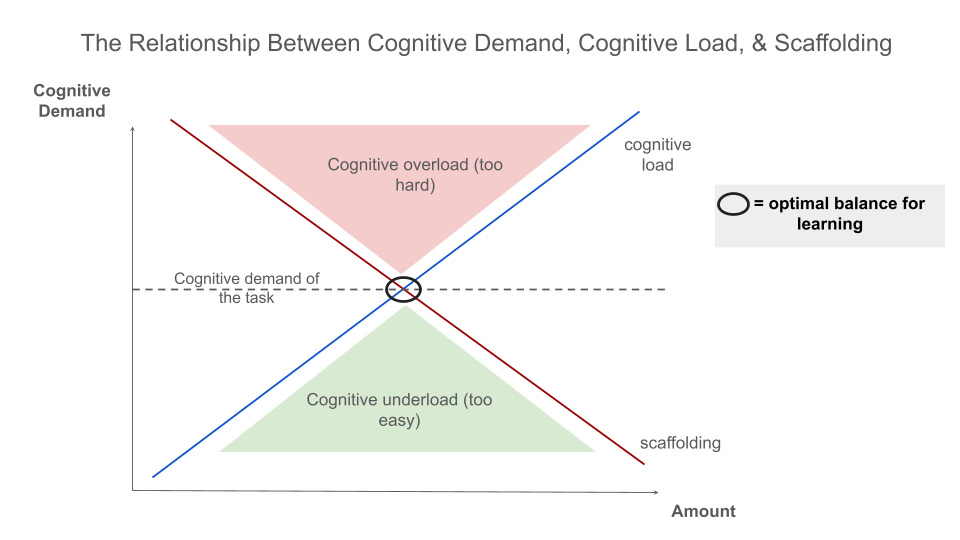
The figure below maps the relationship between cognitive demand, cognitive load, and scaffolding. To maintain a task’s cognitive demand, a teacher must provide just enough scaffolding to prevent students from becoming cognitively overloaded without reducing the effort students must exert to engage with the task. In other words, because scaffolding reduces cognitive load, too much can inadvertently lower the task’s cognitive demand. This inverse relationship makes maintaining high demand a delicate balancing act, with little margin for error.
© Thomas Nobili 2025
When it comes to maintaining cognitive demand, it’s not always the content of the scaffold that matters, it’s often the timing. Teachers frequently jump in too early, sometimes at the first sign of struggle because we see it as our job to be helpful. But this well-intentioned instinct can inadvertently rob students of the opportunity to engage in meaning-making, the process of connecting new ideas to prior knowledge, which is essential for building robust mental schemas.
In many classrooms, struggle is treated as an obstacle to learning rather than a catalyst for it. Yet a substantial body of research shows that students need to grapple meaningfully with challenging mathematical ideas in order to learn deeply (Bjork, 1994; Hiebert & Wearne, 1993; Hiebert & Grouws, 2007; Warshauer, 2015). That said, the term productive struggle is not without controversy. It is sometimes misrepresented as simply letting students flounder by engaging in unstructured discovery with little to no teacher guidance. To avoid such ambiguity, I adopt Hiebert and Grouws’ (2007) operational definition: "The intellectual effort students expend to make sense of mathematical concepts that are challenging but fall within their reasonable capabilities."
According to this view, productive struggle involves students working through challenges that are within reach, a conceptual space described by Vygotsky as the zone of proximal development (ZPD), while being supported thoughtfully and given sufficient time. In fact, research on human-assisted tutoring by VanLehn et al. (2003) found that learning was more likely when students hit an impasse—a moment of not knowing—than when they completed tasks with ease. The study concluded that allowing students to attempt a step, even if they might make a mistake, was more beneficial for learning than preemptively showing them how to do it. This suggests that, at times, the best response to a student who is stuck is to do less, not more. As Peter Liljedahl (2021) puts it, sometimes the most effective move is simply to smile and walk away.
However, when students genuinely need support, responding in the moment is one of the most challenging and uncertain aspects of teaching (Gehrtz, Branter, & Andrews, 2022; Luna & Selmer, 2021). Even when a teacher has successfully surfaced and made sense of student thinking, a difficult task in itself, the next step isn’t straightforward. In these moments, there’s often a strong instinct to correct errors or guide students toward the “right” answer. This reflex is understandable: it’s fast, familiar, and feels helpful. But it can also undermine richer learning opportunities. By jumping in too quickly to correct or direct, we risk missing the chance to build on a partial idea, transform a misconception into a productive turning point, or pose a question that deepens the whole class’s engagement. Learning to pause that instinct and instead respond to student thinking as it is, not as we wish it were, is a complex and essential part of effective practice.
One of the most common ways cognitive demand is unintentionally reduced is through what Henningsen and Stein (1997) refer to as “task devolution”: when the teacher, in an effort to clarify or help, reshapes a rich task into a procedural one. This might involve rephrasing a question to make it simpler, narrowing the number of acceptable strategies, stepping in with a model too soon, or providing hints that remove the need for sensemaking. These responses often emerge from a desire to protect students from failure or frustration, but they come at a cost as they strip away the very cognitive work the task was designed to elicit.
Classroom Connection
Students often reach different kinds of impasses as they engage with challenging mathematical tasks. These points of difficulty are not only expected but can be leveraged as opportunities for meaningful learning. However, the challenge lies in knowing how to support students in ways that manage cognitive load without diminishing the task’s cognitive demand. In this section, I explore two common moments of struggle during task enactment: getting started and carrying out a solution process. For each, I offer specific scaffolds that help students move forward while preserving opportunities for reasoning and sense-making.
Students may experience difficulty early in the lesson, particularly when they struggle to find an entry point into the task. When this happens, it can serve as valuable feedback to the teacher about the effectiveness of the task launch. One of the primary goals of a strong launch is to frame the problem in a way that provides all students with a clear entry point into the work. If multiple students are unable to get started, it may indicate that the launch failed to illuminate a meaningful starting point.
That said, there are also times when a task has been set up for broad accessibility, but students don’t recognize that they can get started. In these cases, teachers have several options for supporting students in ways that preserve the task’s cognitive demand.
First, whenever possible, cognitively demanding tasks should be embedded in a meaningful context. This serves several functions, but most relevant here is that the context can act as a scaffold by making abstract mathematical ideas more concrete, familiar, or meaningful thus reducing cognitive load and helping students access the problem. Let’s use the following example to illustrate this point. Suppose we presented the following question to a third grade class:
You're designing a dog pen for your new puppy. You have 24 feet of fencing. What are some different rectangular shapes you could make for the pen? Which shape gives your puppy the most space to run around?
In this example the context can scaffold student thinking in a few different ways:
The goal (giving the puppy space to run) gives meaning to maximizing area, helping students make sense of why that matters.
The fixed amount of fencing (24 ft) sets a real-world perimeter, providing structure without needing to define "perimeter" explicitly.
Students might start by drawing random sized rectangles or draw on prior experience (i.e. we have a fenced in space for our dog so I’ll start with sketching that shape), before there is a need for formal mathematical reasoning.
Contrast this with,a decontextualized version of this task like "List all rectangles with a perimeter of 24 units. Which has the greatest area?" which may feel overly abstract or confusing to students who haven’t yet developed fluency with the relationship between perimeter and area. So, the context doesn't just decorate the task, it helps students enter it.
Second, teachers can reframe the conversation from what students don’t know to what they do know. For example, after a task launch, a student might raise their hand and say, “I don’t get any of this.” Rather than jumping in with a directive, the teacher might respond, “Tell me one thing you do know about the problem.” Starting from what the student can articulate helps lower extraneous cognitive load and guides them toward initial steps they can take.
Finally, teachers can leverage peer thinking as a scaffold. If a student or group is stuck, the teacher might say, “I see you’re having trouble figuring out how to begin. Go talk to Eddie’s group about how they got started and see if that gives you any ideas.” This kind of strategic redirection not only supports the struggling student, but also promotes knowledge mobility across the classroom.
Another common point during task enactment where students may need support is in carrying out a process that leads to a solution. When this happens, a teacher’s first move should often be to reduce extraneous cognitive load. Specifically, any unnecessary mental effort that interferes with students’ ability to focus on the mathematics at hand. As discussed in my earlier post on cognitive load, this might involve providing tools like a multiplication chart or a list of relevant formulas, so students can devote their cognitive resources to reasoning rather than retrieval.
Sometimes, reducing extraneous load also means supplying a key piece of information necessary for students to engage in the kind of mathematical thinking germane to the lesson. For instance, my colleague Isobel and I recently facilitated a workshop where the topic of background knowledge came up. The group of teachers we were working with expressed concern about how students could engage with a measurement task if they didn’t know how many inches are in a foot. This concern highlights an important instructional distinction: when students are unable to carry out a process because of a missing fact, and they clearly recognize the need for that fact, providing it directly is not a case of reducing cognitive demand, rather it’s clearing the path for deeper engagement. In this case, the struggle is not conceptual; it’s about having access to information required for meaningful sense-making.
This is where the distinction between background knowledge as schema versus background knowledge as isolated facts becomes crucial. When we talk about the importance of activating prior knowledge and its role in managing cognitive load, we are referring to schema, or well-organized networks of connected knowledge, not simply isolated facts.
For example, a student may not know the fact that there are 12 inches in a foot, but this does not mean they lack a schema for the concept of measurement. In fact, they may understand quite a bit: that different units are used to measure different attributes, that some units can be converted into others, and that there are distinctions between standard and non-standard units of measure. So if they are working on a measurement task and get stuck because they don’t know how many inches are in a foot, we should simply tell them because the very fact that they realize they need that information suggests that they are actively reasoning within a robust schema. In this case, they are engaging in measurement conversion, which is a form of proportional reasoning. Withholding that fact in the name of “productive struggle” would misinterpret the nature of maintaining cognitive demand, they don’t need to discover it; they need it as a tool to advance deeper thinking.
In situations where students are struggling to carry out a solution process, but are not overwhelmed by extraneous cognitive load, prompting them to consider a particular strategy or representation can help focus their cognitive effort on the germane aspects of the problem. The key is to avoid simply telling them what to do. For example, if students are stuck on a ratio problem involving the relationship between pounds of wheat and total cost, a teacher might be tempted to say, "You should use a ratio table so you can see how the price increases at the same rate per pound." While this may help the student get an answer, it likely robs them of the opportunity to make sense of the mathematical relationships themselves.
Instead, we want to use the thinking the student has already done as a bridge to deepen their reasoning. Suppose a student has already figured out that 2 pounds of wheat cost $4.46 and 4 pounds cost $8.92, but is struggling to determine the cost of 10 pounds. Rather than introducing a new strategy or representation, we might organize their existing work in a ratio table and ask, “If 2 pounds cost $4.46 and 4 pounds cost $8.92, what do you think 8 pounds would cost?” Since the student already used a doubling strategy from 2 to 4 pounds, they’re likely to double again to find the cost of 8 pounds. From there, we can ask, “So now you have the cost for 2, 4, and 8 pounds. Can you use that information to figure out 10 pounds?” This approach honors the student’s thinking, reinforces the structure in the mathematics, and supports strategic sense-making—all without lowering the cognitive demand of the task.
It’s important to emphasize that the scaffold provided, namely organizing the student’s work into a table and use of strategic prompting, offers access to germane features of the task without constraining the student to a single line of reasoning. The information in the table can be interpreted and extended in multiple ways, depending on how the student is making sense of the problem. For example, a student might:
Combine the costs of 8 pounds and 2 pounds to find the cost of 10 pounds;
Scale the cost for 2 pounds by a factor of 5;
Halve the cost for 2 pounds to find the cost for 1 pound, then multiply by 10;
Use the fact that 10 is 2.5 times 4 to scale up accordingly;
Notice that the cost in each row is consistently 2.23 times the number of pounds and apply that relationship to 10 pounds.
Each of these approaches reflects significant mathematical thinking: unit rate, equivalence, the Distributive Property, scaling, and Constant of Proportionality, and all contribute to building deeper conceptual understanding. The point is not to guide students toward a single “correct” method, but to support and expand the reasoning they’ve already begun.
Supporting students during moments of struggle is one of the most critical and nuanced aspects of teaching. It requires a deep understanding of the relationship between cognitive load and cognitive demand, and a commitment to keeping students intellectually engaged. Whether the challenge lies in getting started or progressing through a solution, the teacher’s role is not to rescue but to reframe, redirect, and refocus while drawing on students’ existing thinking as a bridge to new understanding. When done well, scaffolding doesn’t reduce the challenge of the task; it makes that challenge more accessible. And in doing so, it helps students build the kind of mathematical agency and resilience that meaningful learning requires.
Related Reads
This study examines the different types of productive struggle experienced by a sample of middle school math students and the types of scaffolds teachers employed as a result. The author offers a framework for how to approach scaffolding while maintaining the cognitive demand of the task.
This article provides an extensive review on the research on scaffolding and its connection to Cognitive Load Theory.
This blog post by Julie Dixon, highlights the critical differences between a just-in-case and just-in-time approach to scaffolding.
The study suggests that engaging in specific teaching practices—like building on student thinking—can help mitigate the common tendency to unintentionally lower cognitive demand through over-scaffolding.
This study analyzed what features of student-tutor dialog are associated with learning in a sample of physics students. The authors concluded that successful learning seems to require that the student reach an impasse. When students were not at an impasse, learning was uncommon regardless of the tutorial explanations employed.